What Led Kepler to Discover That Planetary Orbits Are Ellipses?

The Scientific discipline: Orbital Mechanics

Kepler's Laws of Planetary Move

While Copernicus rightly observed that the planets revolve around the Dominicus, it was Kepler who correctly defined their orbits. At the age of 27, Kepler became the assistant of a wealthy astronomer, Tycho Brahe, who asked him to define the orbit of Mars. Brahe had nerveless a lifetime of astronomical observations, which, on his death, passed into Kepler's easily. (Brahe, who had his ain Globe-centered model of the Universe, withheld the bulk of his observations from Kepler at least in part because he did not want Kepler to use them to prove Copernican theory right.) Using these observations, Kepler found that the orbits of the planets followed three laws.

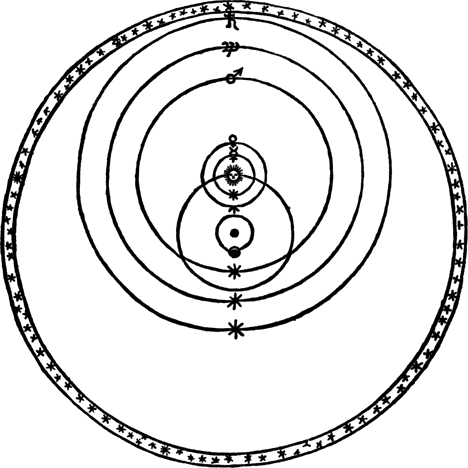
Brahe believed in a model of the Universe with the Dominicus (rayed disk) orbiting the Earth (black dot), just the other planets (symbols) orbiting the Sunday. In an endeavor to prove his theory, Brahe compiled all-encompassing astronomical records, which Kepler eventually used to bear witness heliocentrism and to calculate the orbital laws. [Adapted from Tycho Brahe, Astronomiae instauratae progymnasmata ("Introductory exercises toward the restoration of astronomy.")]

Like many philosophers of his era, Kepler had a mystical belief that the circle was the Universe'due south perfect shape, and that equally a manifestation of Divine order, the planets' orbits must be circular. For many years, he struggled to make Brahe'southward observations of the motions of Mars match up with a circular orbit.

Eventually, yet, Kepler noticed that an imaginary line drawn from a planet to the Sun swept out an equal area of space in equal times, regardless of where the planet was in its orbit. If you draw a triangle out from the Sunday to a planet's position at i bespeak in fourth dimension and its position at a fixed time later—say, 5 hours, or 2 days—the expanse of that triangle is ever the same, anywhere in the orbit. For all these triangles to have the aforementioned expanse, the planet must move more quickly when it is near the Dominicus, but more than slowly when it is uttermost from the Lord's day.

This discovery (which became Kepler'southward second constabulary of orbital motion) led to the realization of what became Kepler'south first law: that the planets move in an ellipse (a squashed circle) with the Sun at one focus bespeak, offset from the heart.

Through Brahe's astronomical measurements and Kepler's own drawings of the geometrical relationship between the Dominicus and Mars in various parts of the planet'southward orbit, Kepler discovered that planets moved faster when they were closer to the Sun. From this realization, he concluded that the orbit of Mars was elliptical, not round. [Adapted from Johannes Kepler, Prototype astronomia Copernicanae ("Epitome of Copernican Astronomy.")]

Kepler'southward third law shows that there is a precise mathematical relationship betwixt a planet's distance from the Sun and the amount of time it takes circumduct around the Sunday. It was this law that inspired Newton, who came up with three laws of his own to explain why the planets motion every bit they do.

Newton's Laws of Movement

If Kepler'southward laws define the motion of the planets, Newton'due south laws ascertain move. Thinking on Kepler'south laws, Newton realized that all motion, whether it was the orbit of the Moon around the Earth or an apple tree falling from a tree, followed the same bones principles. "To the same natural effects," he wrote, "we must, as far as possible, assign the same causes." Previous Aristotelian thinking, physicist Stephen Hawking has written, assigned different causes to different types of motion. By unifying all motion, Newton shifted the scientific perspective to a search for large, unifying patterns in nature. Newton outlined his laws in Philosophiae Naturalis Principia Mathematica ("Mathematical Principles of Natural Philosophy,") published in 1687.

Constabulary I. Every torso perseveres in its state of residuum, or of uniform motility in a right line, unless it is compelled to change that country by forces impressed theron.

In essence, a moving object won't change speed or direction, nor will a yet object start moving, unless some outside strength acts on it. The law is regularly summed upwardly in one discussion: inertia.

Law Ii. The alteration of movement is ever proportional to the motive force impressed; and is fabricated in the direction of the right line in which that force is impressed.

Newton's second law is most recognizable in its mathematical course, the iconic equation: F=ma. The strength of the force (F) is divers by how much information technology changes the motion (acceleration, a) of an object with some mass (m).

Law III. To every action in that location is always opposed an equal reaction: or the mutual deportment of 2 bodies upon each other are e'er equal, and directed to opposite parts.

Every bit Newton himself described: "If yous printing a rock with your finger, the finger is likewise pressed by the stone."

Gravity

Within the pages of Principia, Newton as well presented his police force of universal gravitation as a instance written report of his laws of motility. All matter exerts a strength, which he called gravity, that pulls all other thing towards its center. The forcefulness of the strength depends on the mass of the object: the Sun has more than gravity than Globe, which in plough has more gravity than an apple. Also, the force weakens with distance. Objects far from the Sun won't be influenced by its gravity.

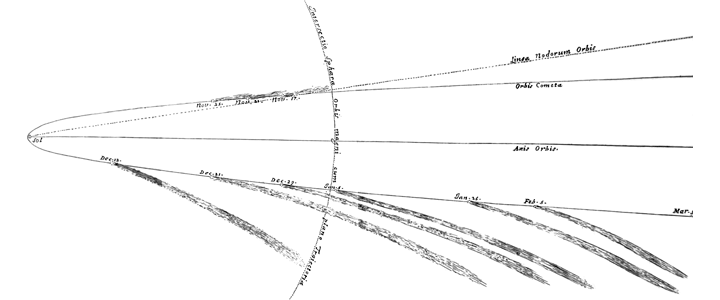
Isaac Newton demonstrated his universal law of gravitation by showing that a comet visible during 1680 and 1681 followed the path of a parabola. [Adapted from Isaac Newton, 1687. Philosophiae Naturalis Principia Mathematica ("Mathematical Principles of Natural Philosophy.")]

Newton'due south laws of motion and gravity explained Earth's almanac journeying around the Sun. Globe would motility straight forrard through the universe, but the Lord's day exerts a constant pull on our planet. This strength bends Earth's path toward the Lord's day, pulling the planet into an elliptical (well-nigh round) orbit. His theories as well made information technology possible to explain and predict the tides. The rise and autumn of sea h2o levels are created by the gravitational pull of the Moon as it orbits Earth.

Einstein and Relativity

The ideas outlined in Newton's laws of motion and universal gravitation stood unchallenged for most 220 years until Albert Einstein presented his theory of special relativity in 1905. Newton's theory depended on the assumption that mass, fourth dimension, and distance are constant regardless of where you measure them.

The theory of relativity treats fourth dimension, space, and mass as fluid things, divers past an observer'south frame of reference. All of us moving through the universe on the Earth are in a unmarried frame of reference, but an astronaut in a fast-moving spaceship would be in a different reference frame.

Within a single frame of reference, the laws of classical physics, including Newton's laws, hold true. But Newton'due south laws can't explain the differences in motion, mass, distance, and time that result when objects are observed from 2 very dissimilar frames of reference. To describe motion in these situations, scientists must rely on Einstein's theory of relativity.

At slow speeds and at large scales, however, the differences in time, length, and mass predicted by relativity are small enough that they appear to exist constant, and Newton's laws still work. In general, few things are moving at speeds fast enough for us to discover relativity. For big, tedious-moving satellites, Newton's laws still define orbits. We tin still use them to launch Earth-observing satellites and predict their movement. Nosotros can utilise them to reach the Moon, Mars, and other places beyond Earth. For this reason, many scientists see Einstein's laws of general and special relativity non as a replacement of Newton's laws of movement and universal gravitation, simply as the full culmination of his idea.

1. References

2. Air Academy. (2003, Baronial). Orbital Mechanics. Infinite Primer. Accessed May 22, 2009.
3. Blitzer, L. (1971, August). Satellite orbit paradox: A general view. American Periodical of Physics, 39, 882-886.
4. Gleick, J. (2003). Isaac Newton. New York: Vintage Books.
5. Gribbon, J. (2008). The Scientists: A History of Science Told Through the Lives of Its Greatest Inventors. New York: Random Business firm.
6. Hawking, S. (2004). The Illustrated on the Shoulders of Giants. Philadelphia: Running Press.
7. Iannotta, B., and Malik, T. (2009, February 11). U.Southward. satellite destroyed in space collision. Accessed May 22, 2009.
8. Komoma. GPS Satellite Orbits. Accessed May 22, 2009.
9. Serway, R.A. (1992). Physics for Scientists and Engineers, third ed. Philadelphia: Saunders College Publishing and Harcourt Brace College Publishers.
10. Wolfe, J., and Hatsidimitris, G. (2005). Einstein Light. University of New S Wales. Accessed June eleven, 2009.

valentinasaing74.blogspot.com

Source: https://earthobservatory.nasa.gov/features/OrbitsHistory/page2.php